The Art of Linear Algebra¶

-- Graphic Notes on “Linear Algebra for Everyone" --¶

作者: Kenji Hiranabe ¹

在 Gilbert Strang ² 的亲切帮助下

译者: Kefang Liu ³

日期: September 1, 2021/updated today

摘要¶

我尝试为 Gilbert Strang 在书籍 “Linear Algebra for Everyone” 中介绍的矩阵的重要概念进行可视化图释, 以促进从矩阵分解的角度对向量、矩阵计算和算法的理解。⁴它们包括矩阵分解 (Column-Row, \(\boldsymbol{CR}\))、高斯消去法 (Gaussian Elimination, \(\boldsymbol{LU}\))、格拉姆-施密特正交化 (Gram-Schmidt Orthogonalization, \(\boldsymbol{QR}\))、特征值和对角化 (Eigenvalues and Diagonalization, \(\boldsymbol{Q \Lambda Q^\mathrm{T}}\))、和奇异值分解 (Singular Value Decomposition, \(\boldsymbol{U \Sigma V^\mathrm{T}}\))。

序言¶

我很高兴能看到 Kenji Hiranabe 的线性代数中的矩阵运算的图片! 这样的图片是展示代数的绝佳方式. 我们当然可以通过行 \(\boldsymbol{\cdot}\) 列的点乘来想象矩阵乘法, 但那绝非全部 —— 它是“线性组合”与“秩1矩阵”组成的代数与艺术. 我很感激能看到日文翻译的书籍和 Kenji 的图片中的想法.

-- Gilbert Strang

麻省理工学院数学教授

目录¶

The Art of Linear Algebra

1、理解矩阵——4个视角¶

一个矩阵 (\(m \times n\)) 可以被视为\(1\)个矩阵, \(mn\)个数, \(n\)个列和\(m\)个行。

从四个角度理解矩阵

图 1: 从四个角度理解矩阵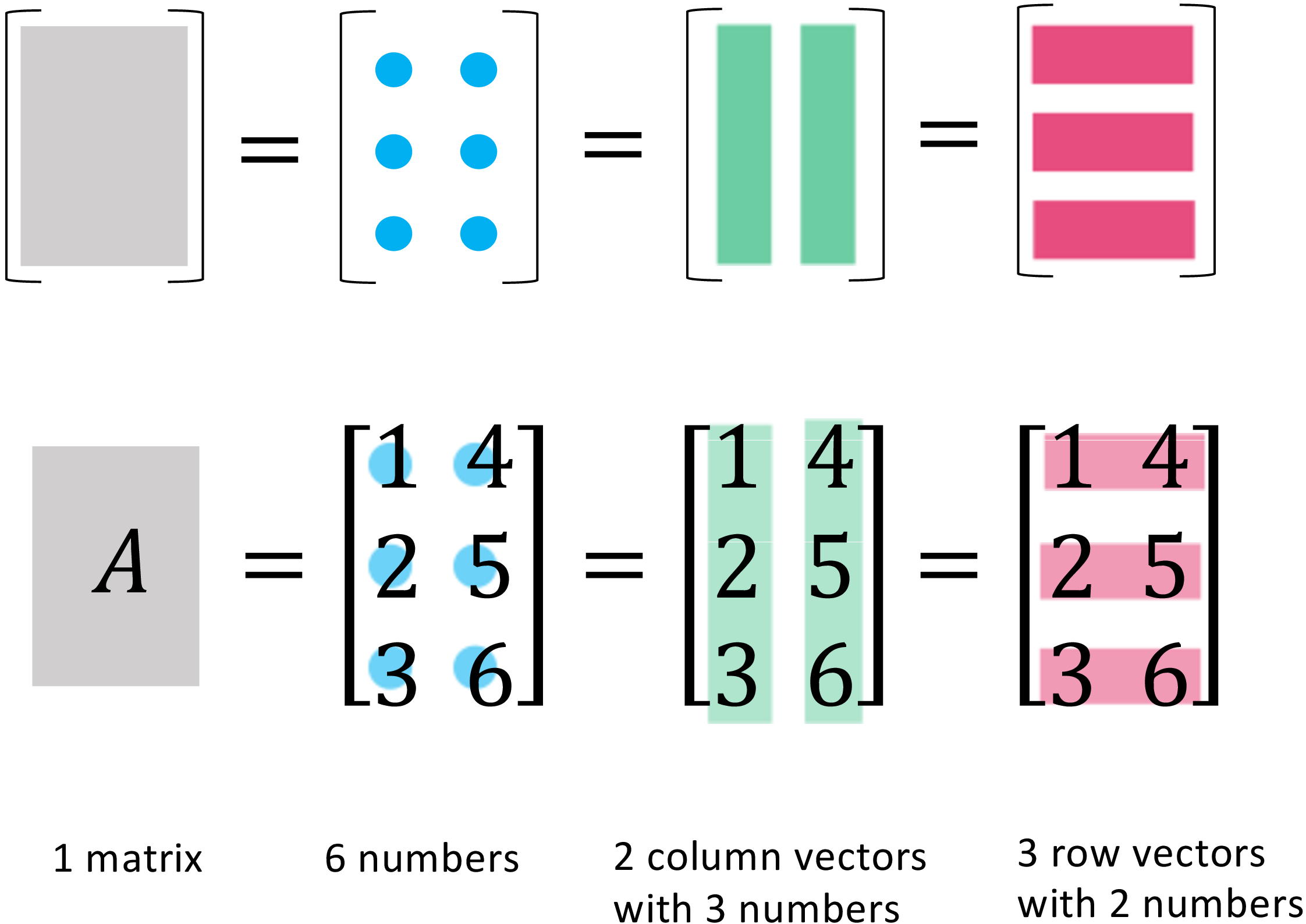

\[ A= \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ a_{31} & a_{32} \end{bmatrix} = \begin{bmatrix} | & |\\ \boldsymbol{a_1} & \boldsymbol{a_2}\\ | & | \end{bmatrix} = \begin{bmatrix} - \boldsymbol{a_1^*} -\\ - \boldsymbol{a_2^*} -\\ - \boldsymbol{a_3^*} - \end{bmatrix} \]

在这里, 列向量被标记为粗体\(\boldsymbol{a_1}\)。行向量则有一个\(\boldsymbol{*}\)号, 标记为\(\boldsymbol{a_1^*}\)。转置向量和矩阵则用\(\mathrm{T}\)标记为\(\boldsymbol{a}^\mathrm{T}\)和\(A^\mathrm{T}\)。

2、向量乘以向量——2个视角¶

后文中, 我将介绍一些概念, 同时列出“Linear Algebra for Everyone”一书中的相应部分 (部分编号插入如下)。详细的内容最好看书, 这里我也添加了一个简短的解释, 以便您可以通过这篇文章尽可能多地理解。

此外, 每个图都有一个简短的名称, 例如 v1 (数字 1 表示向量的乘积)、Mv1 (数字 1 表示矩阵和向量的乘积), 以及如下图 (v1) 所示的彩色圆圈。如你所见, 随着讨论的进行, 该名称将被交叉引用。

1.1节 (p.2) Linear combination and dot products
1.3节 (p.25) Matrix of Rank One
1.4节 (p.29) Row way and column way

向量乘以向量 - (v1), (v2)

图 2: 向量乘以向量 - (v1), (v2)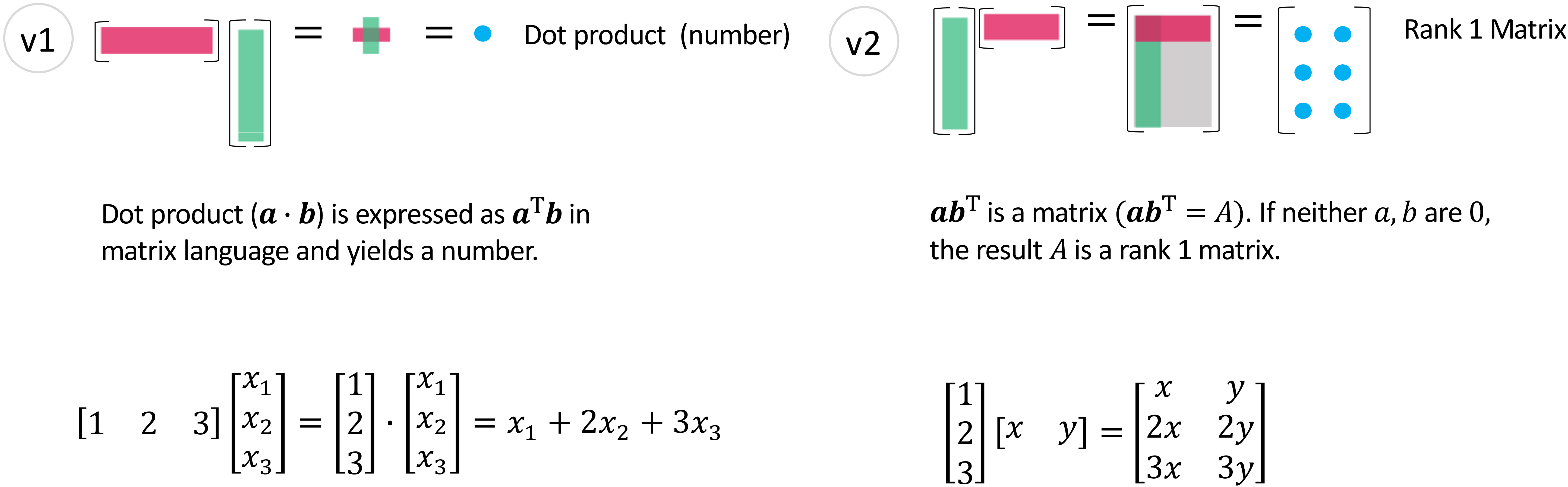

(v1) 是两个向量之间的基础运算, 而 (v2) 将列乘以行并产生一个秩1矩阵。理解 (v2) 的结果 (秩1) 是接下来章节的关键。

3、矩阵乘以向量——2个视角¶

一个矩阵乘以一个向量将产生三个点积组成的向量 (Mv1) 和一种\(A\)的列向量的线性组合。

1.1节 (p.3) Linear combinations
1.3节 (p.21) Matrices and Column Spaces

矩阵乘以向量- (Mv1), (Mv2)

图 3: 矩阵乘以向量- (Mv1), (Mv2)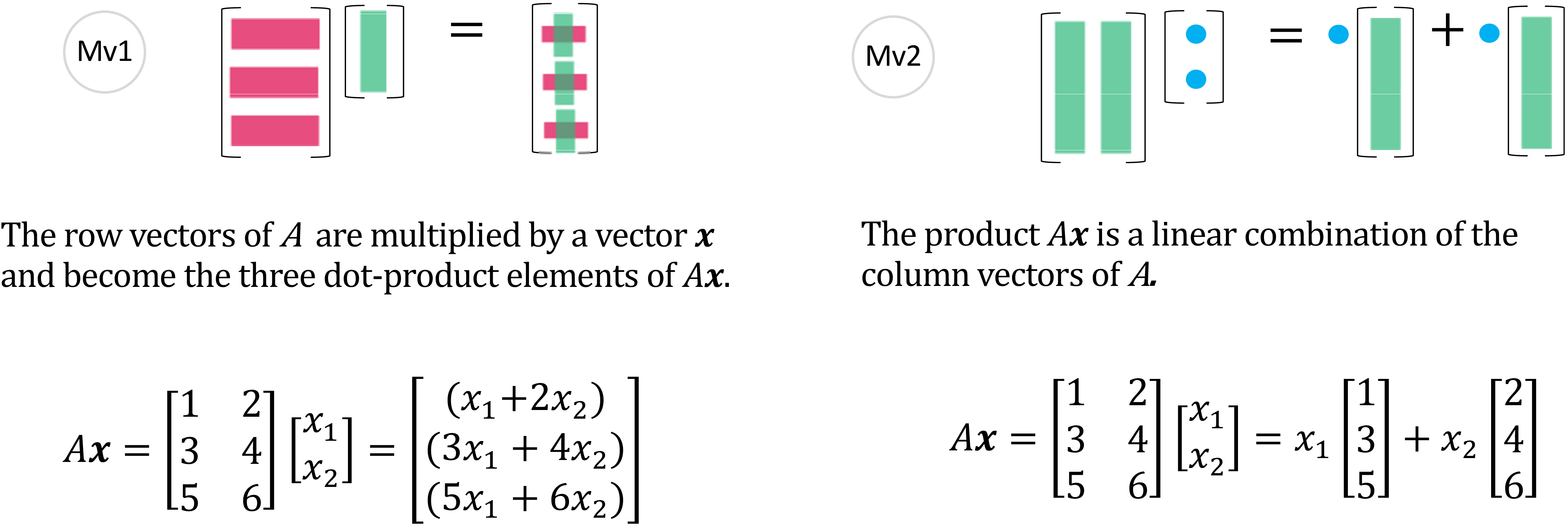

往往你会先学习 (Mv1). 但当你习惯了从 (Mv2) 的视角看待它, 会理解\(A\boldsymbol{x}\)是\(A\)的列的线性组合。矩阵\(A\)的列向量的所有线性组合生成的子空间记为\(\boldsymbol{C}(A)\)。\(A\boldsymbol{x}=\boldsymbol{0}\)的解空间则是零空间, 记为\(\boldsymbol{N}(A)\)。

同理, 由 (vM1) 和 (vM2) 可见, 行向量乘以矩阵也是同一种理解方式。

向量乘以矩阵 - (vM1), (vM2)

图 4: 向量乘以矩阵 - (vM1), (vM2)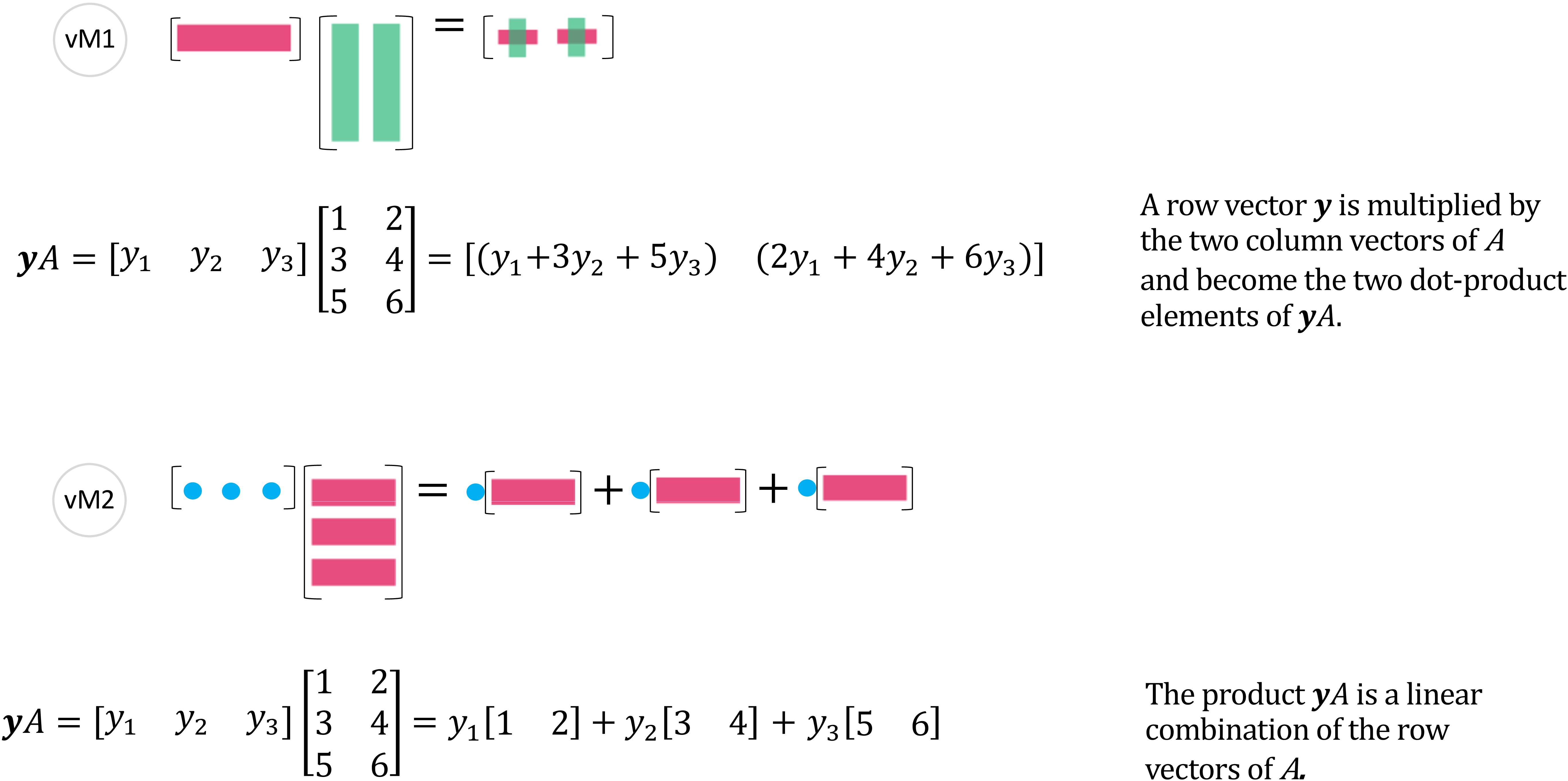

上图\(A\)的行向量的所有线性组合生成的子空间记为\(\boldsymbol{C}(A^\mathrm{T})\)。\(yA=0\)的解空间是\(A\)的左零空间, 记为 \(\boldsymbol{N}(A^\mathrm{T})\)。

本书的一大亮点即为四个基本子空间: 在\(\mathbb{R}^n\) 上的\(\boldsymbol{N}(A)\) + \(\boldsymbol{C}(A^\mathrm{T})\) (相互正交) 和在\(\mathbb{R}^m\) 上的\(\boldsymbol{N}(A^\mathrm{T})\) + \(\boldsymbol{C}(A)\) (相互正交)。

3.5节 (p.124) Dimensions of the Four Subspaces

四个子空间

图 5: 四个子空间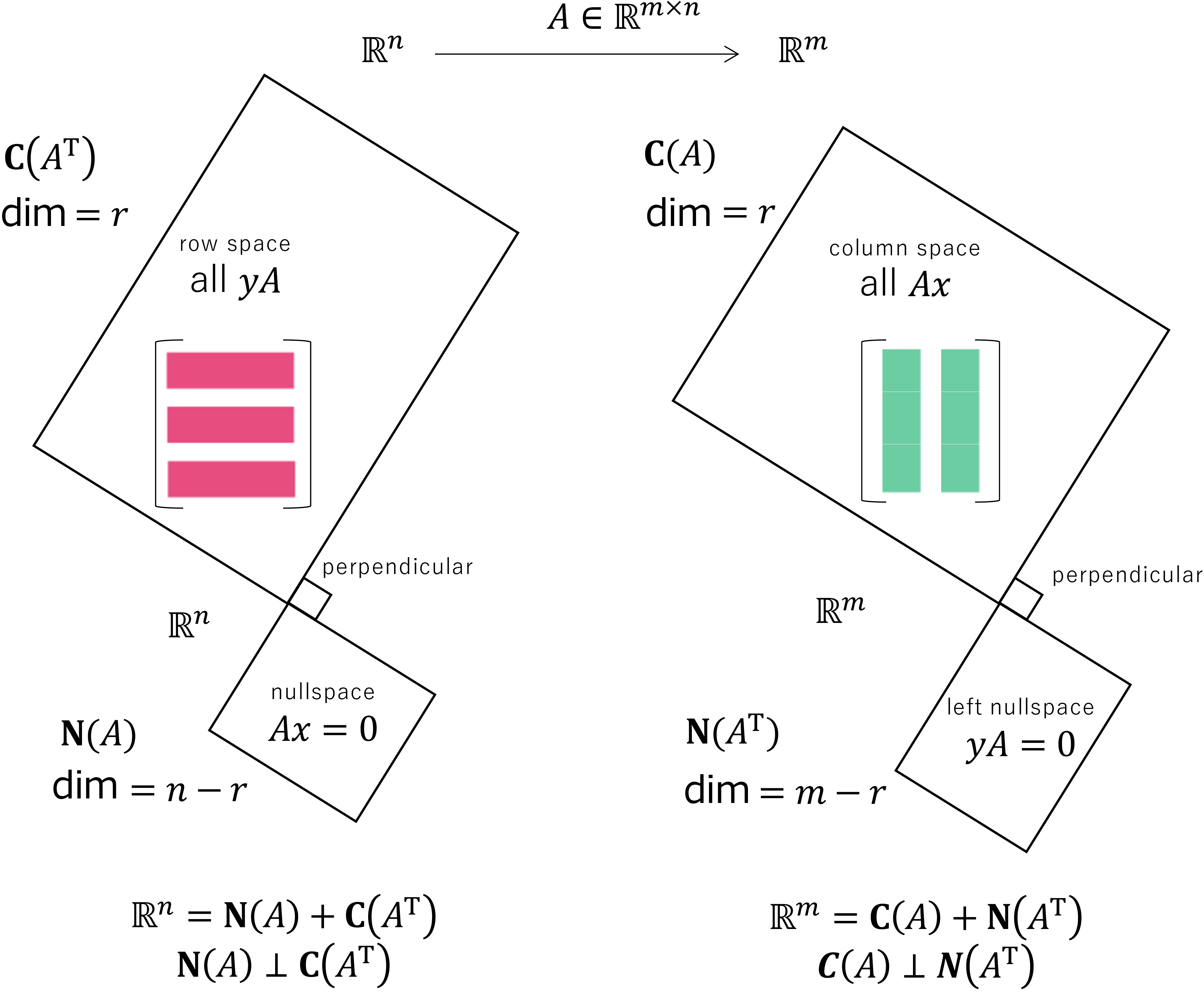

关于秩\(r\), 请见\(A=CR\) (6.1节)。

4、矩阵乘以矩阵——4个视角¶

由矩阵乘以向量"自然延伸到矩阵乘以矩阵"。

1.4节 (p.35) Four ways to multiply \(\boldsymbol{AB=C}\)
也可以见书的封底

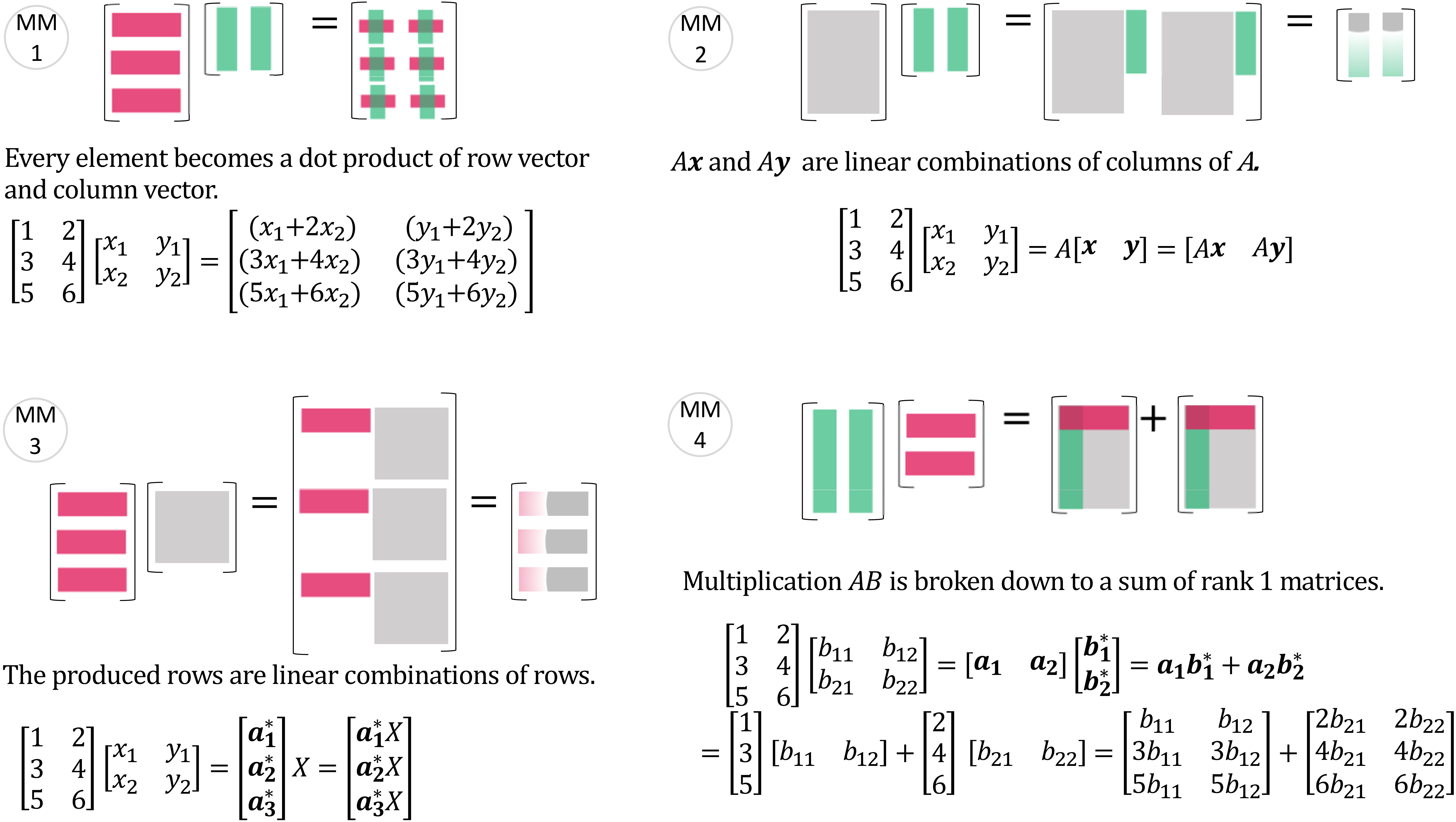
矩阵乘以矩阵 - (MM1), (MM2), (MM3), (MM4)

图 6: 矩阵乘以矩阵 - (MM1), (MM2), (MM3), (MM4)

5、实用模式¶

在这里, 我展示了一些实用的模式, 可以让你更直观地理解接下来的内容。

图 1, 2 - (P1), (P1)

图 7: 图 1, 2 - (P1), (P1)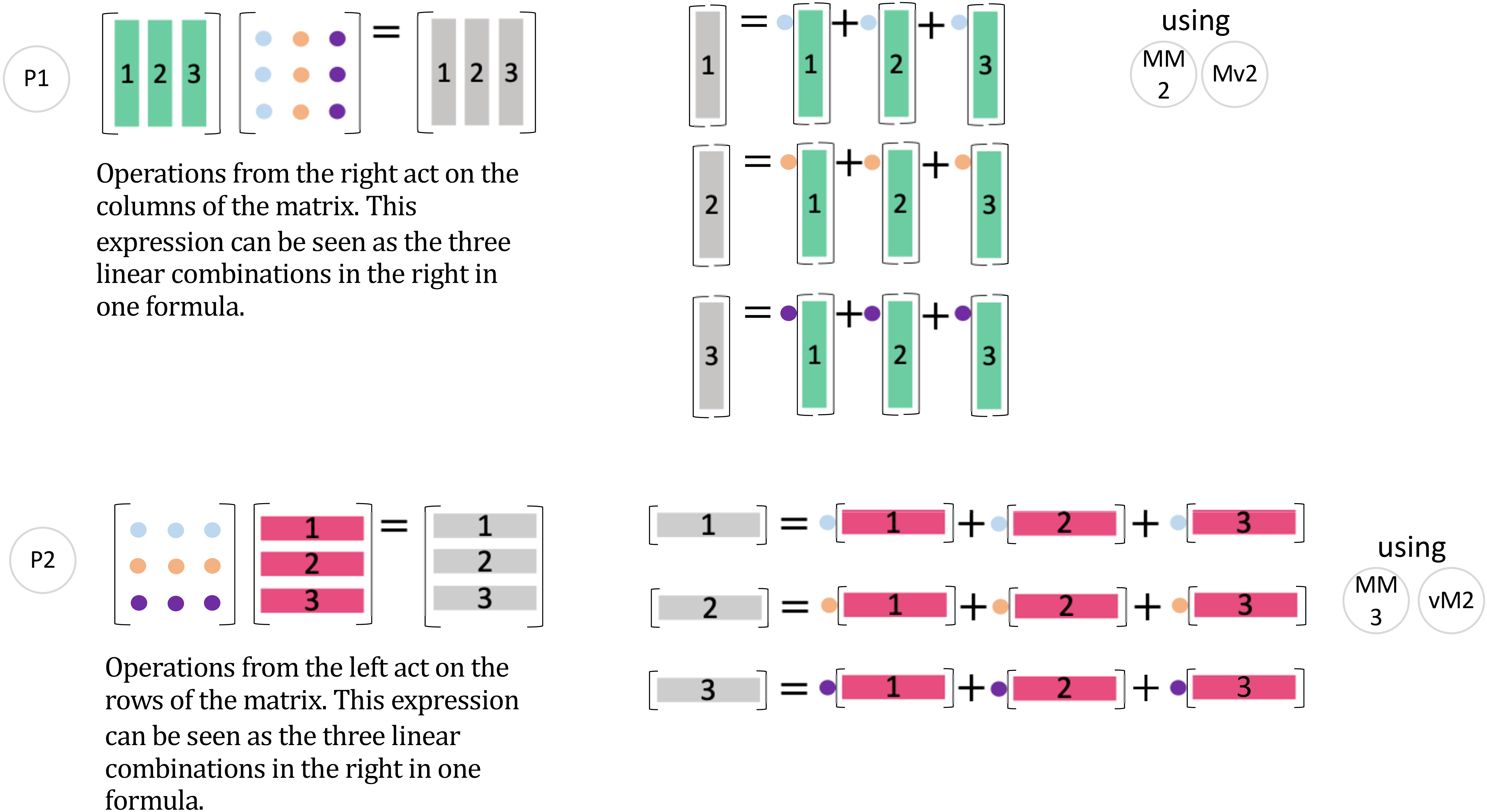

P1 是 (MM2) 和 (Mv2) 的结合。P2 是 (MM3) 和 (vM2) 的扩展。注意, P1 是列运算 (右乘一个矩阵), 而 P2 是行运算 (左乘一个矩阵)。

图 1′, 2′ - (P1′), (P2′)

图 8: 图 1′, 2′ - (P1′), (P2′)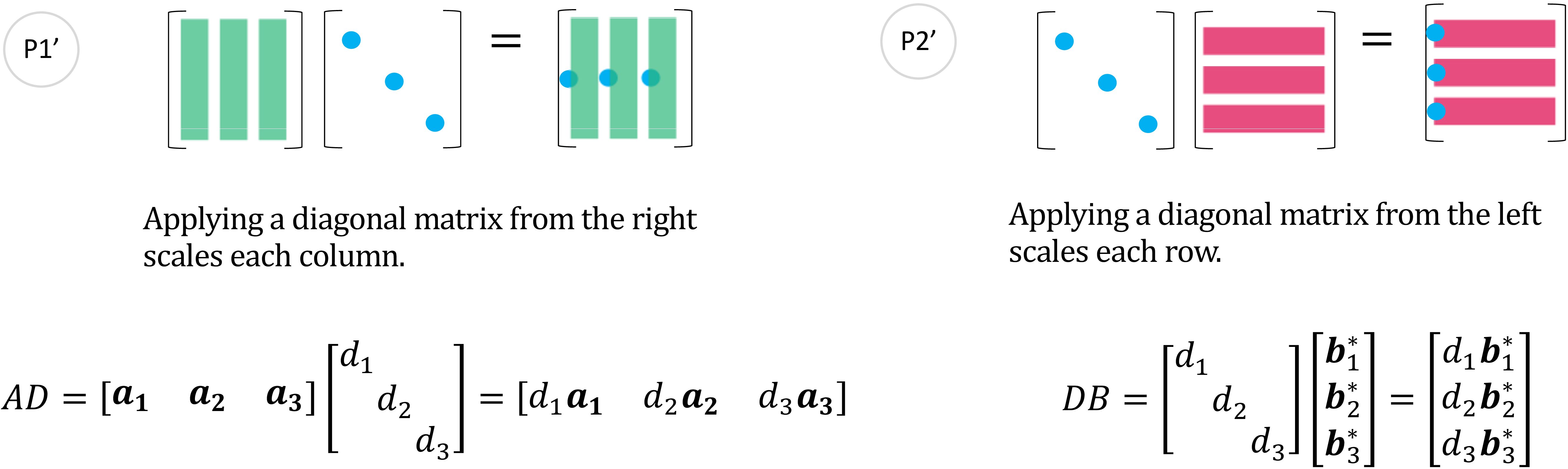

(P1′) 将对角线上的数乘以矩阵的列, 而 (P2′) 将对角线上的数乘以矩阵的行。两个分别为 (P1) 和 (P2) 的变体。

图 3 - (P3)

图 9: 图 3 - (P3)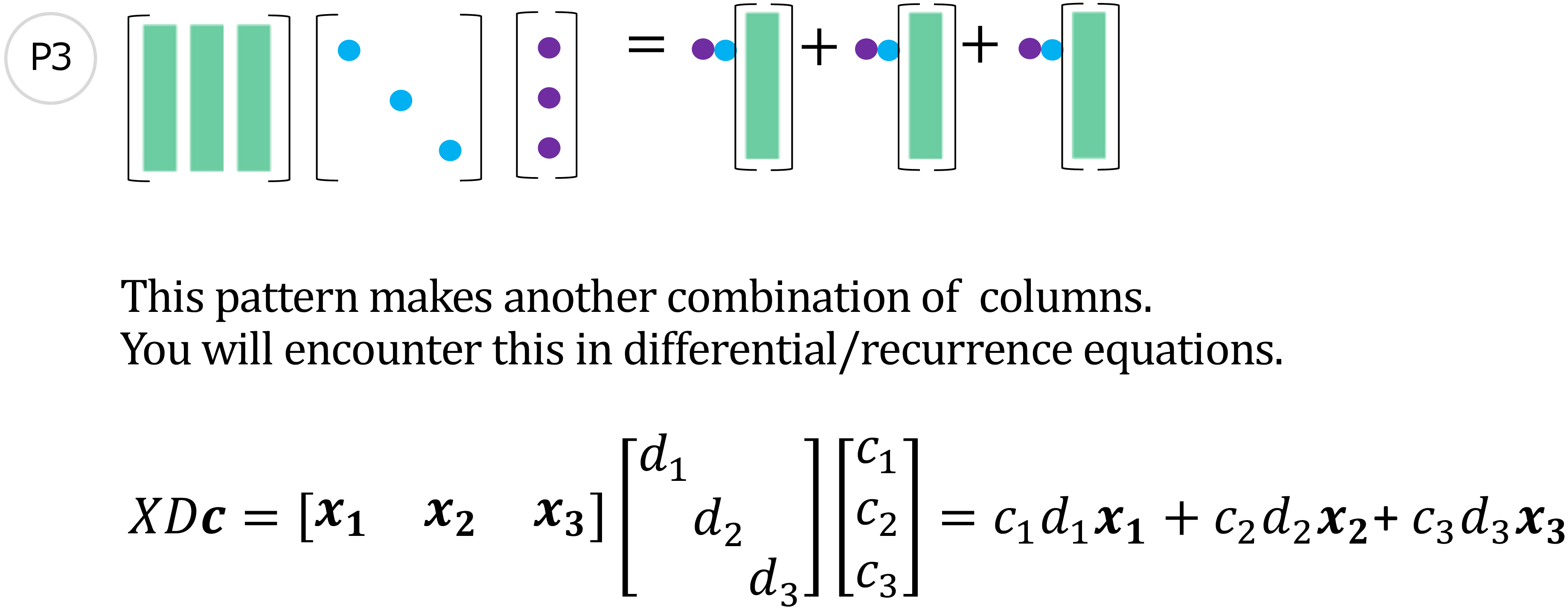

当解决微分方程和递归方程时的也会出现这一模式:

6节 (p.201) Eigenvalues and Eigenvectors
6.4节 (p.243) Systems of Differential Equations

\[ \begin{aligned} \frac{d \boldsymbol{u}(t) }{dt} &= A \boldsymbol{u}(t), \quad \boldsymbol{u}(0)=\boldsymbol{u}_0\\ \boldsymbol{u}_{n+1} &= A \boldsymbol{u}_n, \quad \boldsymbol{u_0} = \boldsymbol{u}_0 \end{aligned} \]

在两种问题中, 它的解都可以用\(A\)的特征值(\(\lambda_1, \lambda_2, \lambda_3\))、特征向量\(X=\begin{bmatrix} \boldsymbol{x}_1 & \boldsymbol{x}_2 & \boldsymbol{x}_3 \end{bmatrix}\)和系数\(c=\begin{bmatrix} c_1 & c_2 & c_3 \end{bmatrix}^\mathrm{T}\)表示。其中\(C\)是以\(X\)为基底的初始值\(\boldsymbol{u}(0)=\boldsymbol{u}_0\)的坐标。

\[ \boldsymbol{u}_0 = c_1 \boldsymbol{x}_1 + c_2 \boldsymbol{x}_2 + c_3 \boldsymbol{x}_3 \]

\[ \boldsymbol{c} = \begin{bmatrix} c_1\\ c_2\\ c_3 \end{bmatrix} = X^{-1} \boldsymbol{u}_0 \]

以上两个问题的通解为:

\[ \begin{aligned} \boldsymbol{u}(t) &= e^{At} \boldsymbol{u}_0 = X e^{\Lambda t} X^{-1} \boldsymbol{u_0} &= X e^{\Lambda t} \boldsymbol{c} &= c_1 e^{\lambda_1 t} \boldsymbol{x}_1 + c_2 e^{\lambda_2 t} \boldsymbol{x}_2 + c_3 e^{\lambda_3 t} \boldsymbol{x}_3\\ \boldsymbol{u}_n &= A^n \boldsymbol{u}_0 = X \Lambda^n X^{-1} \boldsymbol{u_0} &= X \Lambda^n \boldsymbol{c} &= c_1 \lambda_1^n \boldsymbol{x}_1 + c_2 \lambda_2^n \boldsymbol{x}_2 + c_3 \lambda_3^n \boldsymbol{x}_3 \end{aligned} \]

见图 9: 通过P3可以得到\(XDc\)。

Pattern 4 - (P4)

图 10: Pattern 4 - (P4)

P4在特征值分解和特异值分解中都会用到。两种分解都可以表示为三个矩阵之积, 其中中间的矩阵均为对角矩阵。且都可以表示为带特征值/特异值系数的秩1矩阵之积。

更多细节将在下一节中讨论。

6、矩阵的五种分解¶

前言 p.vii, The Plan for the Book.

\(A=CR, A=LU, A=QR, A=Q \Lambda Q^\mathrm{T}, A=U \Sigma V^\mathrm{T}\) 将一一说明。

分解	图示	说明
\(\boldsymbol{A=CR}\)		\(C\)为\(A\)的线性无关列 \(R\)为\(A\)的行阶梯形矩阵可推知列秩 = 行秩
\(\boldsymbol{A=LU}\)		\(LU\)分解通过高斯消去法 (下三角)(上三角)
\(\boldsymbol{A=QR}\)		\(QR\)分解为格拉姆-施密特正交化中的正交矩阵\(Q\)和三角矩阵\(R\)
\(\boldsymbol{S=Q\Lambda Q^\mathrm{T}}\)		对称矩阵\(S\)可以进行特征值分解特征向量组成\(Q\), 特征值组成\(\Lambda\)
\(\boldsymbol{A=U\Sigma V^\mathrm{T}}\)		所有矩阵\(A\)的奇异值分解奇异值组成\(\Sigma\)

表 1: 五种分解

6.1 \(\boldsymbol{A=CR}\)¶

1.4节 Matrix Multiplication and \(\boldsymbol{A=CR}\) (p.29)

所有一般的长矩阵\(A\)都有相同的行秩和列秩。这个分解是理解这一定理最直观的方法。\(C\)由\(A\)的线性无关列组成, \(R\)为\(A\)的行阶梯形矩阵 (消除了零行)。\(A=CR\)将\(A\)化简为\(r\)的线性无关列\(C\)和线性无关行\(R\)的乘积。

\[ \begin{aligned} A &= CR\\ \begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 5 \end{bmatrix} & = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{bmatrix} \end{aligned} \]

推导过程: 从左往右看\(A\)的列. 保留其中线性无关的列, 去掉可以由前者线性表出的列。则第1、2列被保留, 而第三列因为可以由前两列之和表示而被去掉。而要通过线性无关的1、2两列重新构造出\(A\), 需要右乘一个行阶梯矩阵\(R\)。

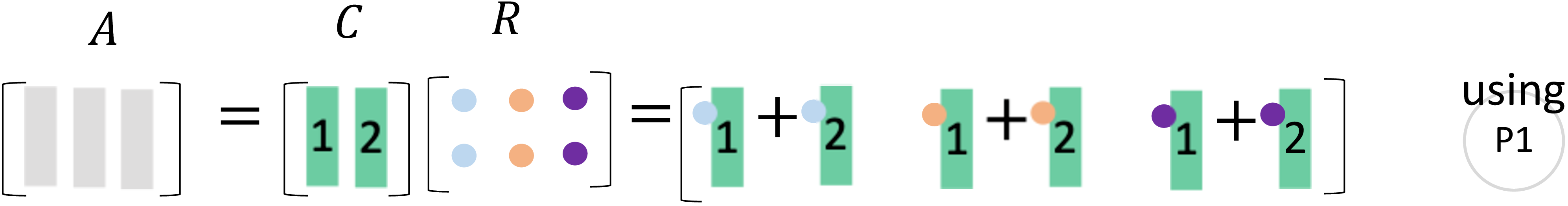
CR中列的秩

图 11: CR中列的秩

现在你会发现列的秩为2, 因为\(C\)中只有2个线性无关列。而\(A\)中所有的列都可以由\(C\)中的2列线性表出。

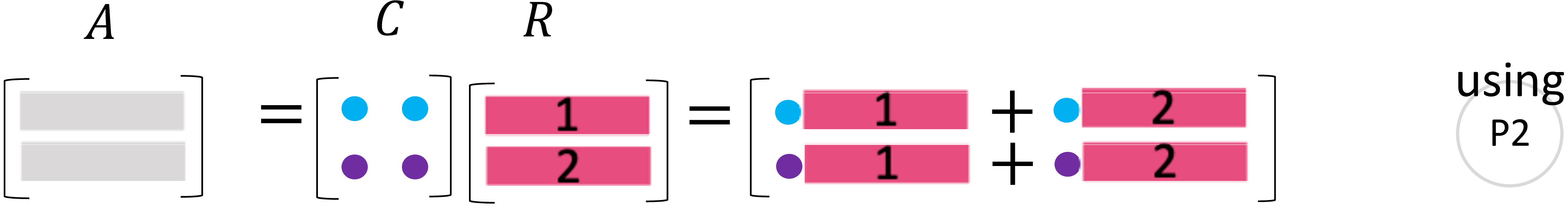
CR中行的秩

图 12: CR中行的秩

同样, 行秩也为2, 因为\(R\)中只有2个线性无关行, 且\(A\)中所有的行都可以由\(R\)中的2行线性表出。

6.2 \(\boldsymbol{A=LU}\)¶

用高斯消除法求解\(A\boldsymbol{x}=\boldsymbol{b}\)也被称为\(LU\)分解。通常, 是\(A\)左乘一个初等行变换矩阵(\(E\))来得到一个上三角矩阵\(U\)。

\[ \begin{aligned} EA &= U\\ A &= E^{-1}U\\ \text{let} \; L = E^{-1}, \quad A &= LU \end{aligned} \]

现在, 求解\(A\boldsymbol{x}=\boldsymbol{b}\)有2步: (1)求解\(L\boldsymbol{c}=\boldsymbol{b}\), (2)代回\(U\boldsymbol{x}=\boldsymbol{c}\)。

2.3节 (p.57) Matrix Computations and \(\boldsymbol{A=LU}\)

在这里, 我们直接通过\(A\)计算\(L\)和\(U\)。

\[ A = \begin{bmatrix} |\\ \boldsymbol{l}_1\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{u}^*_1 - \end{bmatrix} + \begin{bmatrix} 0 & \begin{matrix} 0 & 0 \end{matrix}\\ \begin{matrix} 0 \\ 0 \end{matrix} & A_2 \end{bmatrix} = \begin{bmatrix} |\\ \boldsymbol{l}_1\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{u}^*_1 - \end{bmatrix} + \begin{bmatrix} |\\ \boldsymbol{l}_2\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{u}^*_2 - \end{bmatrix} + \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & A_3 \end{bmatrix} = LU \]

A的递归秩1矩阵分离

图 13: \(A\)的递归秩1矩阵分离

要计算\(L\)和\(U\), 首先分离出由\(A\)的第一行和第一列组成的外积。余下的部分为\(A_2\)。递归执行此操作, 将\(A\)分解为秩1矩阵之和。

由LU重新构造A

图 14: 由\(LU\)重新构造\(A\)

由\(L\)乘以\(U\)来重新构造\(A\)则相对简单。

6.3\(\boldsymbol{A=QR}\)¶

\(A=QR\)是在保持\(\boldsymbol{C}(A) = \boldsymbol{C}(Q)\)的条件下, 将\(A\)转化为正交矩阵\(Q\)。

4.4节 Orthogonal matrices and Gram-Schmidt (p.165)

在格拉姆-施密特正交化中, 首先, 单位化的\(\boldsymbol{a}_1\)被用作\(\boldsymbol{q}_1\), 然后求出\(\boldsymbol{a}_2\)与\(\boldsymbol{q}_1\)正交所得到的\(\boldsymbol{q}_2\), 以此类推。

\[ \begin{aligned} \boldsymbol{q}_1 &= \boldsymbol{a}_1/||\boldsymbol{a}_1|| \\ \boldsymbol{q}_2 &= \boldsymbol{a}_2 - (\boldsymbol{q}_1^\mathrm{T} \boldsymbol{a}_2)\boldsymbol{q}_1 , \quad \boldsymbol{q}_2 = \boldsymbol{q}_2/||\boldsymbol{q}_2|| \\ \boldsymbol{q}_3 &= \boldsymbol{a}_3 - (\boldsymbol{q}_1^\mathrm{T} \boldsymbol{a}_3)\boldsymbol{q}_1 - (\boldsymbol{q}_2^\mathrm{T} \boldsymbol{a}_3)\boldsymbol{q}_2, \quad \boldsymbol{q}_3 = \boldsymbol{q}_3/||\boldsymbol{q}_3|| \end{aligned} \]

或者你也可以写作\(r_{ij} = \boldsymbol{q}_i^\mathrm{T} \boldsymbol{a}_j\):

\[ \begin{aligned} \boldsymbol{a}_1 &= r_{11}\boldsymbol{q}_1\\ \boldsymbol{a}_2 &= r_{12}\boldsymbol{q}_1 + r_{22} \boldsymbol{q}_2\\ \boldsymbol{a}_3 &= r_{13}\boldsymbol{q}_1 + r_{23} \boldsymbol{q}_2 + r_{33} \boldsymbol{q}_3 \end{aligned} \]

原本的\(A\)就可以表示为\(QR\): 正交矩阵乘以上三角矩阵。

\[ \begin{gathered} A = \begin{bmatrix} | & | & |\\ \boldsymbol{q}_1 & \boldsymbol{q}_2 & \boldsymbol{q}_3\\ | & | & | \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13}\\ & r_{22} & r_{23}\\ & & r_{33} \end{bmatrix} = QR\\ \\ Q Q^\mathrm{T}=Q^\mathrm{T} Q = I \end{gathered} \]

A=QR

图 15: \(A=QR\)

\(A\)的列向量就可以转化为一个正交集合: \(Q\)的列向量。\(A\)的每一个列向量都可以用\(Q\)和上三角矩阵\(R\)重新构造出。

图释可以回头看P1。

6.4 \(\boldsymbol{S=Q \Lambda Q^\mathrm{T}}\)¶

所有对称矩阵\(S\)都必须有实特征值和正交特征向量。特征值是\(\Lambda\)的对角元素, 特征向量在\(Q\)中。

6.3节 (p.227) Symmetric Positive Definite Matrices

\[ \begin{aligned} S = Q \Lambda Q^\mathrm{T} &= \begin{bmatrix} | & | & |\\ \boldsymbol{q}_1 & \boldsymbol{q}_2 & \boldsymbol{q}_3\\ | & | & | \end{bmatrix} \begin{bmatrix} \lambda_1 \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} \begin{bmatrix} - \boldsymbol{q}_1^\mathrm{T} -\\ - \boldsymbol{q}_2^\mathrm{T} -\\ - \boldsymbol{q}_3^\mathrm{T} - \end{bmatrix}\\ \\ &= \lambda_1 \begin{bmatrix} |\\ \boldsymbol{q}_1\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{q}_1^\mathrm{T} - \end{bmatrix} + \lambda_2 \begin{bmatrix} |\\ \boldsymbol{q}_2\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{q}_2^\mathrm{T} - \end{bmatrix} + \lambda_3 \begin{bmatrix} |\\ \boldsymbol{q}_3 \\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{q}_3^\mathrm{T} - \end{bmatrix} \\ &= \lambda_1 P_1 + \lambda_2 P_2 + \lambda_3 P_3 \end{aligned} \]

\[ P_1=\boldsymbol{q}_1 \boldsymbol{q}_1^\mathrm{T}, \quad P_2=\boldsymbol{q}_2 \boldsymbol{q}_2^\mathrm{T}, \quad P_3=\boldsymbol{q}_3 \boldsymbol{q}_3^\mathrm{T} \]

S=Q Λ Qᵀ

图 16: \(S=Q \Lambda Q^\mathrm{T}\)

一个对称矩阵\(S\)通过一个正交矩阵\(Q\)和它的转置矩阵, 对角化为\(\Lambda\)。然后被分解为秩一投影矩阵\(P=qq^\mathrm{T}\)的组合。这就是谱定理。

注意, 这里的分解用到了P4。

\[ \begin{gathered} S=S^\mathrm{T} = \lambda_1 P_1 + \lambda_2 P_2 + \lambda_3 P_3\\ QQ^\mathrm{T} = P_1 + P_2 + P_3 = I \\ P_1 P_2 = P_2 P_3 = P_3 P_1 = O\\ P_1^2 =P_1=P_1^\mathrm{T}, \quad P_2^2=P_2=P_2^\mathrm{T}, \quad P_3^2=P_3=P_3^\mathrm{T} \end{gathered} \]

6.5 \(\boldsymbol{A=U \Sigma V^\mathrm{T}}\)¶

7.1节 (p.259) Singular Values and Singular Vecrtors

包括长方阵在内的所有矩阵都具有奇异值分解(SVD)。\(A=U \Sigma V^\mathrm{T}\)中, 有\(A\)的奇异向量\(U\)和\(V\)。奇异值则排列在\(\Sigma\)的对角线上。下图就是“简化版”的SVD。

A=U Σ Vᵀ

图 17: \(A=U \Sigma V^\mathrm{T}\)

你可以发现, \(V\)是\(\mathbb{R}^n\) (\(A^\mathrm{T} A\)的特征向量) 的标准正交基, 而\(U\)是 \(\mathbb{R}^m\) (\(AA^\mathrm{T}\)的特征向量) 的标准正交基。它们共同将\(A\)对角化为\(\Sigma\)。这也可以表示为秩1矩阵的线性组合。

\[ \begin{aligned} A = U \Sigma V^\mathrm{T} &= \begin{bmatrix} | & | & |\\ \boldsymbol{u}_1 & \boldsymbol{u}_2 & \boldsymbol{u}_3\\ | & | & | \end{bmatrix} \begin{bmatrix} \sigma_1 \\ & \sigma_2 \\ & & \end{bmatrix} \begin{bmatrix} - \boldsymbol{v}_1^\mathrm{T} -\\ - \boldsymbol{v}_2^\mathrm{T} - \end{bmatrix} & = \sigma_1 \begin{bmatrix} |\\ \boldsymbol{u}_1\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{v}_1^\mathrm{T} - \end{bmatrix} + \sigma_2 \begin{bmatrix} |\\ \boldsymbol{u}_2\\ | \end{bmatrix} \begin{bmatrix} - \boldsymbol{v}_2^\mathrm{T} - \end{bmatrix} \\ & = \sigma_1 \boldsymbol{u}_1 \boldsymbol{v}_1^\mathrm{T} + \sigma_2 \boldsymbol{u}_2 \boldsymbol{v}_2^\mathrm{T} \end{aligned} \]

注意:

\[ \begin{aligned} U U^\mathrm{T} &= I_m \\ V V^\mathrm{T} &= I_n \end{aligned} \]

图释见P4。

总结和致谢¶

我展示了矩阵/向量乘法的系统可视化与它们在五种矩阵分解中的应用。我希望你能够喜欢它们、通过它们加深对线性代数的理解。

Ashley Fernandes 在排版时帮我美化了这篇论文, 使它更加一致和专业。

在结束这篇论文之前, 我要感谢 Gilbert Strang 教授出版了《Linear Algebra for Everyone》一书。它引导我们通过新的视角去了解线性代数中这些美丽的风景。其中介绍了当代和传统的数据科学和机器学习, 每个人都可以通过实用的方式对它的基本思想进行基本理解。矩阵世界的重要组成部分。

参考文献与相关工作¶

Gilbert Strang(2020), Linear Algebra for Everyone, Wellesley Cambridge Press.,http://math.mit.edu/everyone
Gilbert Strang(2016), Introduction to Linear Algebra, Wellesley Cambridge Press, 5th ed.,http://math.mit.edu/linearalgebra
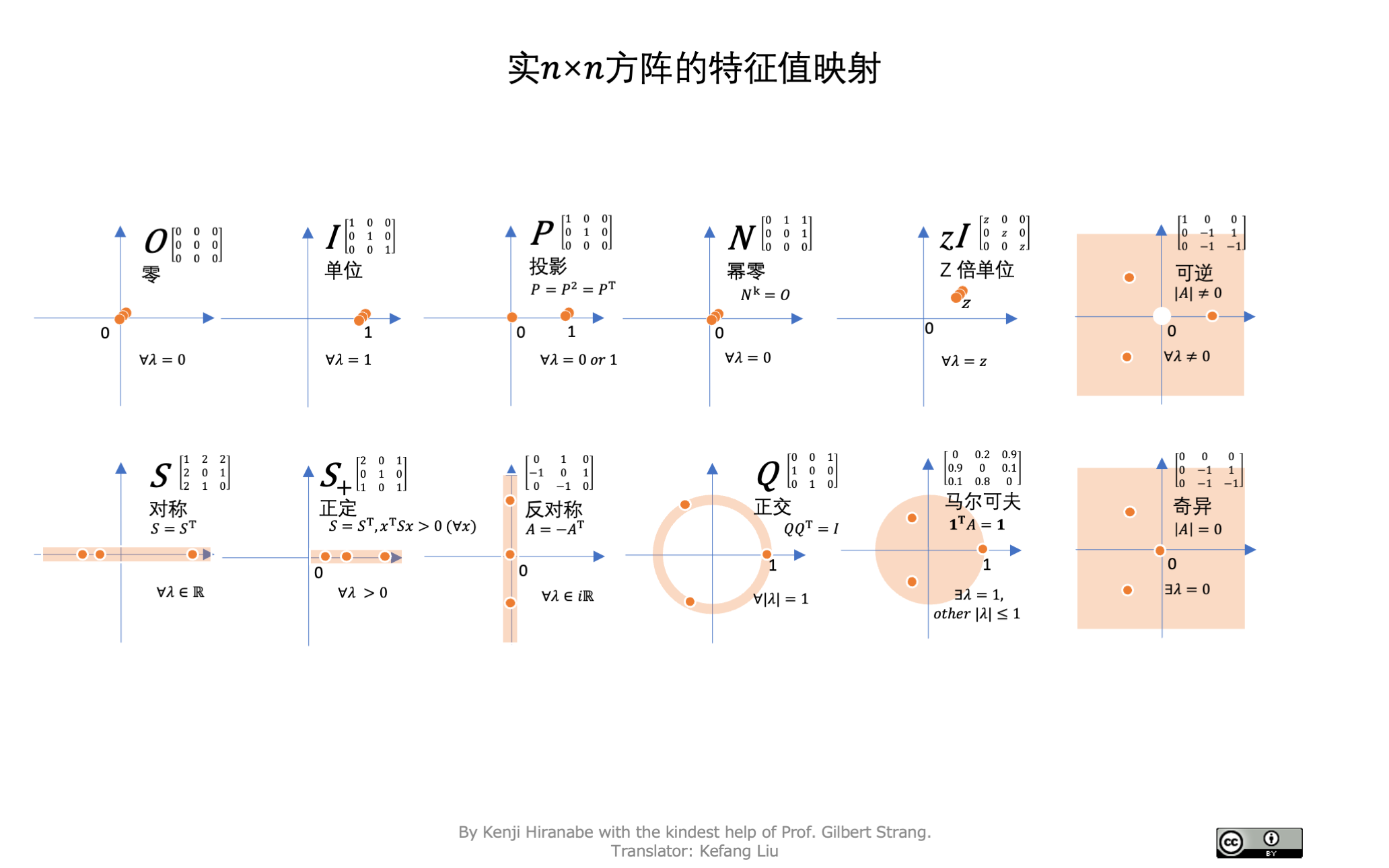
Kenji Hiranabe(2021), Map of Eigenvalues, An Agile Way(blog),https://anagileway.com/2021/10/01/map-of-eigenvalues/ 图 18: 特征值图
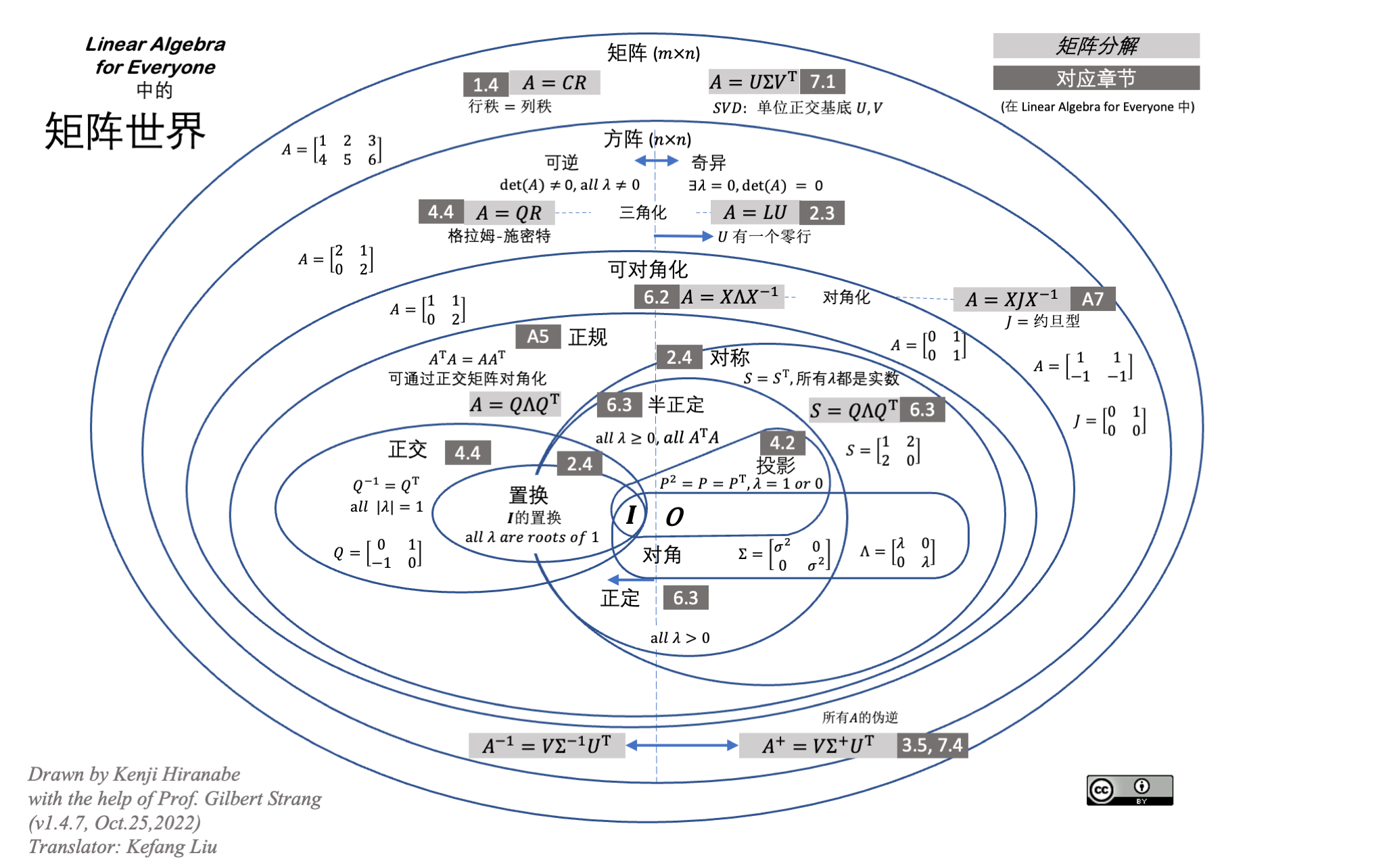
Kenji Hiranabe(2020), Matrix World, An Agile Way(blog),\ https://anagileway.com/2020/09/29/matrix-world-in-linear-algebra-for-everyone/ 图 19: 矩阵世界

twitter: @hiranabe, k-hiranabe@esm.co.jp, https://anagileway.com ↩
Massachusetts Institute of Technology, http://www-math.mit.edu/~gs/ ↩
twitter: @kfchliu, 微博用户: 5717297833 ↩
“Linear Algebra for Everyone": http://math.mit.edu/everyone/. ↩