Skip to content

使用支持向量回归器进行时间序列预测

在上一课中，你学习了如何使用ARIMA模型进行时间序列预测。现在你将学习支持向量回归器模型，这是一种用于预测连续数据的回归模型。

课前测验

引言

在本课程中，你将探索一种使用SVM：Support Vector Machine（支持向量机）构建回归模型的特定方法，即SVR：Support Vector Regressor（支持向量回归器）。

时间序列背景下的SVR 1

在理解SVR在时间序列预测中的重要性之前，你需要了解以下一些重要概念：

  • 回归（Regression）： 一种监督学习技术，用于从一组给定的输入中预测连续值。其思想是在特征空间中拟合一条能包含最多数据点的曲线（或直线）。点击这里了解更多信息。
  • 支持向量机（Support Vector Machine, SVM）： 一种监督式机器学习模型，用于分类、回归和异常值检测。该模型是特征空间中的一个超平面，在分类任务中充当边界，在回归任务中充当最佳拟合线。在SVM中，通常使用核函数将数据集转换到更高维度的空间，使其更容易被分离。点击这里了解更多关于SVM的信息。
  • 支持向量回归器（Support Vector Regressor, SVR）： SVM的一种，用于找到能包含最多数据点的最佳拟合线（在SVM中为超平面）。

为什么选择SVR？1

在上一课中，你学习了ARIMA，这是一种非常成功的用于预测时间序列数据的统计线性方法。然而，在许多情况下，时间序列数据具有非线性特征，这是线性模型无法捕捉的。在这种情况下，SVM在回归任务中考虑数据非线性的能力使得SVR在时间序列预测中取得了成功。

练习 - 构建一个SVR模型

数据准备的前几个步骤与上一课ARIMA的步骤相同。

打开本课的 _/working_ 文件夹，找到 _notebook.ipynb_ 文件。2

  1. 运行 notebook 并导入必要的库：2

    Python
    import sys
sys.path.append('../../')
    Python
    import os
import warnings
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import math

from sklearn.svm import SVR
from sklearn.preprocessing import MinMaxScaler
from common.utils import load_data, mape

  2. 从 /data/energy.csv 文件中加载数据到 Pandas dataframe 并查看：2

    Python
    energy = load_data('../../data')[['load']]

  3. 绘制从2012年1月到2014年12月所有可用的能源数据：2

    Python
    energy.plot(y='load', subplots=True, figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()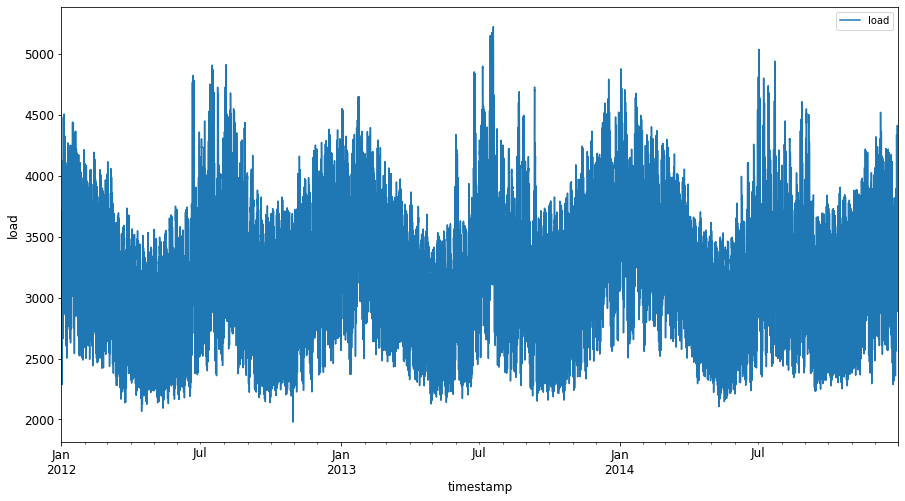

    完整数据

    现在，让我们开始构建SVR模型。

创建训练和测试数据集

数据加载后，你可以将其分为训练集和测试集。然后，你将重塑数据以创建一个基于时间步的数据集，这是SVR所需要的。你将在训练集上训练你的模型。模型训练完成后，你将在训练集、测试集和完整数据集上评估其准确性，以观察其整体性能。你需要确保测试集的时间段晚于训练集，以确保模型不会从未来的时间段获取信息2（这种情况称为过拟合）。

  1. 将2014年9月1日至10月31日这两个月的时间段分配给训练集。测试集将包括2014年11月1日至12月31日这两个月的时间段：2

    Python
    train_start_dt = '2014-11-01 00:00:00'
test_start_dt = '2014-12-30 00:00:00'

  2. 可视化差异：2

    Python
    energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)][['load']].rename(columns={'load':'train'}) \
    .join(energy[test_start_dt:][['load']].rename(columns={'load':'test'}), how='outer') \
    .plot(y=['train', 'test'], figsize=(15, 8), fontsize=12)
plt.xlabel('timestamp', fontsize=12)
plt.ylabel('load', fontsize=12)
plt.show()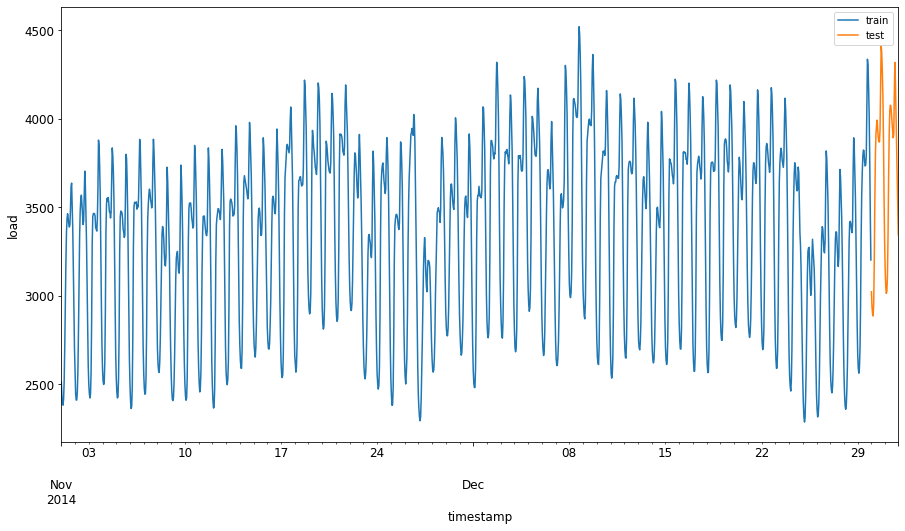

    训练和测试数据

准备用于训练的数据

现在，你需要通过筛选和缩放数据来为训练做准备。筛选你的数据集，只包括所需的时间段和列，并通过缩放确保数据被投射到0到1的区间内。

  1. 筛选原始数据集，使其只包含每个集合的上述时间段，并且只包括所需的 'load' 列和日期：2

    Python
    train = energy.copy()[(energy.index >= train_start_dt) & (energy.index < test_start_dt)][['load']]
test = energy.copy()[energy.index >= test_start_dt][['load']]

print('Training data shape: ', train.shape)
print('Test data shape: ', test.shape)
    Text Output
    Training data shape:  (1416, 1)
Test data shape:  (48, 1)

  2. 将训练数据缩放到 (0, 1) 范围内：2

    Python
    scaler = MinMaxScaler()
train['load'] = scaler.fit_transform(train)

  3. 现在，你缩放测试数据：2

    Python
    test['load'] = scaler.transform(test)

创建带时间步的数据 1

对于SVR，你需要将输入数据转换为 [批次, 时间步] 的形式。因此，你需要重塑现有的 train_data 和 test_data，增加一个代表时间步的新维度。

Python
# 转换为 numpy 数组
train_data = train.values
test_data = test.values

在本例中，我们取 timesteps = 5。因此，模型的输入是前4个时间步的数据，输出将是第5个时间步的数据。

Python
timesteps=5

使用嵌套列表推导式将训练数据转换为2D张量：

Python
train_data_timesteps=np.array([[j for j in train_data[i:i+timesteps]] for i in range(0,len(train_data)-timesteps+1)])[:,:,0]
train_data_timesteps.shape
Text Output
(1412, 5)

将测试数据转换为2D张量：

Python
test_data_timesteps=np.array([[j for j in test_data[i:i+timesteps]] for i in range(0,len(test_data)-timesteps+1)])[:,:,0]
test_data_timesteps.shape
Text Output
(44, 5)

从训练和测试数据中选择输入和输出：

Python
x_train, y_train = train_data_timesteps[:,:timesteps-1],train_data_timesteps[:,[timesteps-1]]
x_test, y_test = test_data_timesteps[:,:timesteps-1],test_data_timesteps[:,[timesteps-1]]

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
Text Output
(1412, 4) (1412, 1)
(44, 4) (44, 1)

实现SVR 1

现在，是时候实现SVR了。要了解更多关于此实现的信息，你可以参考这篇文档。对于我们的实现，我们遵循以下步骤：

  1. 通过调用 SVR() 并传入模型超参数（kernel, gamma, C 和 epsilon）来定义模型。
  2. 通过调用 fit() 函数为训练数据准备模型。
  3. 通过调用 predict() 函数进行预测。

现在我们创建一个SVR模型。这里我们使用RBF核函数，并将超参数gamma, C和epsilon分别设置为0.5, 10和0.05。

Python
model = SVR(kernel='rbf',gamma=0.5, C=10, epsilon = 0.05)

在训练数据上拟合模型 1

Python
model.fit(x_train, y_train[:,0])
Text Output
SVR(C=10, cache_size=200, coef0=0.0, degree=3, epsilon=0.05, gamma=0.5,
    kernel='rbf', max_iter=-1, shrinking=True, tol=0.001, verbose=False)

进行模型预测 1

Python
y_train_pred = model.predict(x_train).reshape(-1,1)
y_test_pred = model.predict(x_test).reshape(-1,1)

print(y_train_pred.shape, y_test_pred.shape)
Text Output
(1412, 1) (44, 1)

你已经构建了你的SVR！现在我们需要评估它。

评估你的模型 1

为了进行评估，我们首先将数据还原到原始尺度。然后，为了检查性能，我们将绘制原始和预测的时间序列图，并打印MAPE结果。

缩放预测值和原始输出：

Python
# 缩放预测值
y_train_pred = scaler.inverse_transform(y_train_pred)
y_test_pred = scaler.inverse_transform(y_test_pred)

print(len(y_train_pred), len(y_test_pred))
Python
# 缩放原始值
y_train = scaler.inverse_transform(y_train)
y_test = scaler.inverse_transform(y_test)

print(len(y_train), len(y_test))

检查模型在训练和测试数据上的性能 1

我们从数据集中提取时间戳，以显示在图的x轴上。请注意，我们使用前 timesteps-1 个值作为第一个输出的输入，所以输出的时间戳将从那之后开始。

Python
train_timestamps = energy[(energy.index < test_start_dt) & (energy.index >= train_start_dt)].index[timesteps-1:]
test_timestamps = energy[test_start_dt:].index[timesteps-1:]

print(len(train_timestamps), len(test_timestamps))
Text Output
1412 44

绘制训练数据的预测图：

Python
plt.figure(figsize=(25,6))
plt.plot(train_timestamps, y_train, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(train_timestamps, y_train_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.title("Training data prediction")
plt.show()

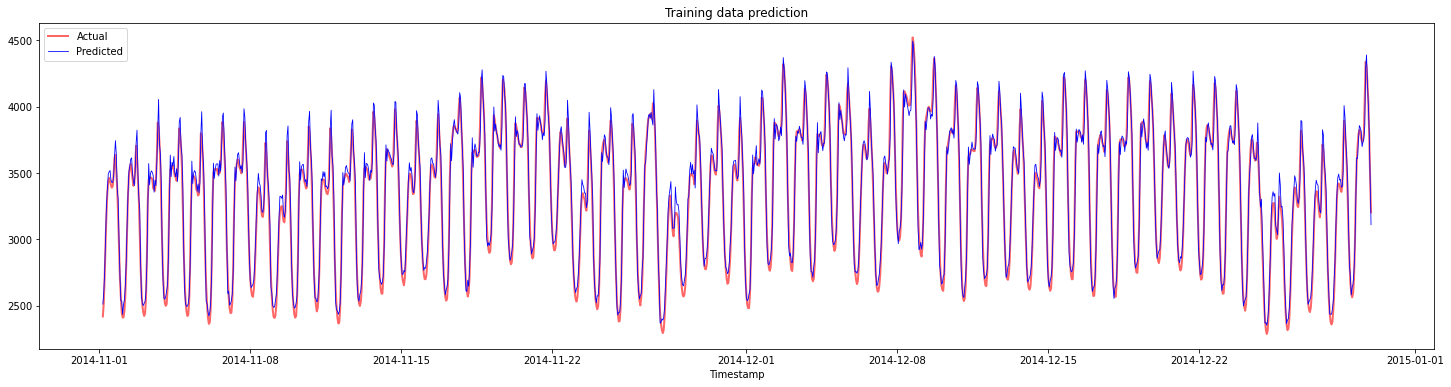
训练数据预测

打印训练数据的MAPE

Python
print('MAPE for training data: ', mape(y_train_pred, y_train)*100, '%')
Text Output
MAPE for training data: 1.7195710200875551 %

绘制测试数据的预测图

Python
plt.figure(figsize=(10,3))
plt.plot(test_timestamps, y_test, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(test_timestamps, y_test_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

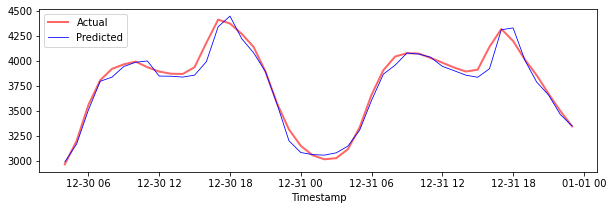
测试数据预测

打印测试数据的MAPE

Python
print('MAPE for testing data: ', mape(y_test_pred, y_test)*100, '%')
Text Output
MAPE for testing data:  1.2623790187854018 %

🏆 你在测试数据集上得到了一个非常好的结果！

检查模型在完整数据集上的性能 1

Python
# 提取load值作为numpy数组
data = energy.copy().values

# 缩放
data = scaler.transform(data)

# 根据模型输入要求转换为2D张量
data_timesteps=np.array([[j for j in data[i:i+timesteps]] for i in range(0,len(data)-timesteps+1)])[:,:,0]
print("Tensor shape: ", data_timesteps.shape)

# 从数据中选择输入和输出
X, Y = data_timesteps[:,:timesteps-1],data_timesteps[:,[timesteps-1]]
print("X shape: ", X.shape,"\nY shape: ", Y.shape)
Text Output
Tensor shape:  (26300, 5)
X shape:  (26300, 4) 
Y shape:  (26300, 1)
Python
# 进行模型预测
Y_pred = model.predict(X).reshape(-1,1)

# 反向缩放和重塑
Y_pred = scaler.inverse_transform(Y_pred)
Y = scaler.inverse_transform(Y)
Python
plt.figure(figsize=(30,8))
plt.plot(Y, color = 'red', linewidth=2.0, alpha = 0.6)
plt.plot(Y_pred, color = 'blue', linewidth=0.8)
plt.legend(['Actual','Predicted'])
plt.xlabel('Timestamp')
plt.show()

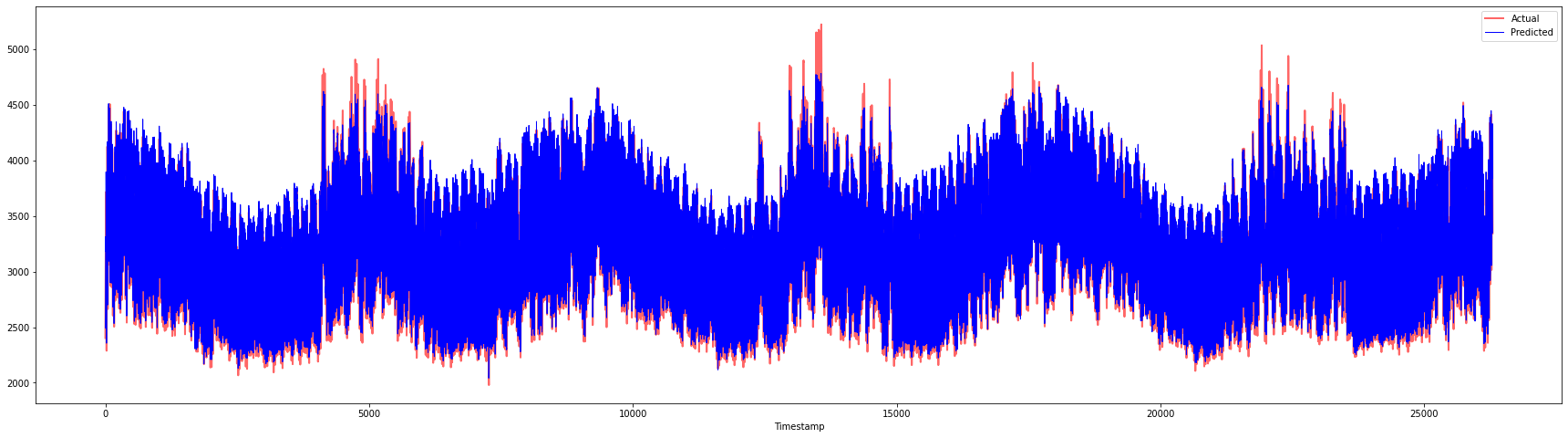
完整数据预测

Python
print('MAPE: ', mape(Y_pred, Y)*100, '%')
Text Output
MAPE:  2.0572089029888656 %

🏆 非常漂亮的图表，显示模型具有良好的准确性。做得好！

🚀挑战

  • 尝试在创建模型时调整超参数（gamma, C, epsilon），并在数据上进行评估，看看哪组超参数在测试数据上能得到最好的结果。要了解更多关于这些超参数的信息，可以参考这篇文档。
  • 尝试为模型使用不同的核函数，并分析它们在数据集上的性能。可以在这里找到一份有用的文档。
  • 尝试使用不同的 timesteps 值，让模型回顾不同长度的历史数据来进行预测。

课后测验

复习与自学

本课旨在介绍SVR在时间序列预测中的应用。要了解更多关于SVR的信息，你可以参考这篇博客。这份scikit-learn上的文档对SVMs整体、SVRs以及其他实现细节，如可以使用的不同核函数及其参数，提供了更全面的解释。

任务

一个新的SVR模型

致谢

  1. 本节中的文本、代码和输出由@AnirbanMukherjeeXD贡献。 ↩↩↩↩↩↩↩↩↩

  2. 本节中的文本、代码和输出取自ARIMA。 ↩↩↩↩↩↩↩↩↩↩