C++递归¶

假设你必须给一些球上色。如果你一个人做，会花费很多时间。你可以做的一件事是向朋友寻求帮助。假设你们的工作速度相同，任务将在一半的时间内完成。现在，你不仅可以向一个朋友寻求帮助，还可以向多个朋友寻求帮助，这样每个朋友只需要给一个球上色。与你自己做相比，任务会完成得更快。递归是一种解决问题的方法，它的工作原理与此类似。

C++递归¶

C++中的递归是一种技术，其中函数反复调用自身，直到给定条件满足。换句话说，递归是通过将问题分解为更小、更简单的子问题来解决问题的过程。

递归的语法结构¶

return_type recursive_func {
    ....
       // Base Condition
       // Recursive Case
       ....
}

递归函数¶

调用自身的函数称为递归函数。当调用递归函数时，它执行一组指令，然后调用自身以使用更小的输入执行相同的指令集。这个过程一直持续到达到基本情况，这是一个停止递归并返回值的条件。

基本情况¶

基本情况是用于终止递归的条件。递归函数将继续调用自身，直到满足基本情况。

递归情况¶

递归情况是递归调用出现在函数中的方式。递归情况可以包含多个递归调用，或不同的参数，以便最终满足基本情况并终止递归。

C++递归示例¶

以下C++程序说明了如何执行递归。

// C++ Program to calculate the sum of first N natural
// numbers using recursion
#include <iostream>
using namespace std;

int nSum(int n)
{
    // base condition to terminate the recursion when N = 0
    if (n == 0) {
        return 0;
    }

    // recursive case / recursive call
    int res = n + nSum(n - 1);

    return res;
}

int main()
{
    int n = 5;

    // calling the function
    int sum = nSum(n);

    cout << "Sum = " << sum;
    return 0;
}

输出

Sum = 15

在上面的示例中，

• 递归函数:nSum()是递归函数
• 递归情况: 表达式int res = n + nSum(n – 1)是递归情况。
• 基本情况: 基本情况是if (n == 0) { return 0;}

C++递归的工作原理¶

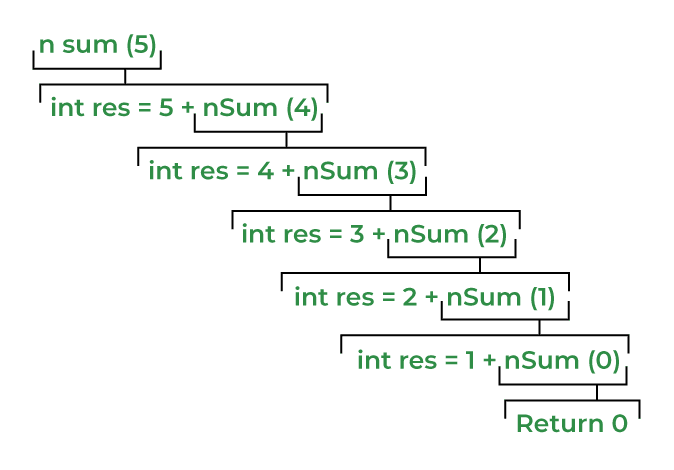
为了理解C++递归的工作原理，我们将再次参考上面的示例并跟踪程序的流程。

1. 在nSum()函数中，递归情况是

int res = n + nSum(n - 1);

1. 在示例中，n = 5，因此根据nSum(5)的递归情况，我们得到

int res = 5 + nSum(4);

3.在nSum(4)中，递归情况和所有其他内容将相同，但n = 4。让我们评估n = 4的递归情 况，

int res = 4 + nSum(3);

4.同样地，对于nSum(3), nSum(2)和nSum(1)

int res = 3 + nSum(2);    // nSum(3)
int res = 2 + nSum(1);    // nSum(2)
int res = 1 + nSum(0);    // nSum(1)

现在让我们不评估nSum(0)及以后的内容。

5.现在回想一下，nSum()函数的返回值是名为res的整数。因此，我们可以用这些函数返回的值代替函数。因此，对于nSum(5)，我们得到

int res = 5 + 4 + nSum(3);

6.同样地，为每个n放入nSum()的返回值，我们得到

int res = 5 + 4 + 3 + 2 + 1 + nSum(0);

1. 在nSum()函数中，基本情况是

if (n == 0) {
    return 0;
}

这意味着当nSum(0)将返回0。将这个值放入nSum(5)的递归情况中，我们得到

int res = 5 + 4 + 3 + 2 + 1 + 0;
        = 15

8.在这一点上，我们可以看到递归情况中没有剩余的函数调用。因此，递归将在这里停止，函数返回的最终值将是15，这是前5个自然数的和。

C++递归中的内存管理¶

与其他所有函数一样，递归函数的数据以堆栈帧的形式存储在堆栈内存中。一旦函数返回某个值，这个堆栈帧就会被删除。在递归中，

• 在返回值之前进行函数调用，因此递归调用的堆栈帧存储在堆栈内存中现有堆栈帧的顶部。
• 当最顶层的函数副本返回某个值时，其堆栈帧被销毁，控制权返回到在为顶层副本进行递归调用之后紧接的特定副本。
• 编译器维护一个指令指针，以跟踪函数执行后返回的位置。

让我们考虑上面的示例并理解nSum(5)函数的内存管理。

步骤1: When nSum() is called from the main() function with 5 as an argument, a stack frame for nSum(5) is created.

步骤2： 在执行nSum(5)时，遇到递归调用作为nSum(4)。编译器现在将在nSum(5)的堆栈帧之上创建一个新的堆栈帧，并在遇到nSum(4)的语句处维护一个指令指针。

步骤3： nSum(4)的执行将开始，但与前一个函数一样，我们遇到另一个递归调用作为nSum(3)。编译器将再次执行相同的步骤，并为nSum(3)维护另一个指令指针和堆栈帧。

步骤4： 同样的事情也会发生在nSum(3)、nSum(2)和nSum(1)的执行中。

步骤5：但当控制权到达nSum(0)时，条件(n == 0)变为真，执行语句return 0。

步骤6：由于nSum(0)返回了值，nSum(0)的堆栈帧将被销毁，并且使用指令指针，程序控制将返回到nSum(1)函数，nSum(0)调用将被值0替换。

步骤7：现在，在nSum(1)中，表达式int res = 1 + 0将被评估，并且执行语句return res。程序控制将使用其指令指针移动到nSum(2)。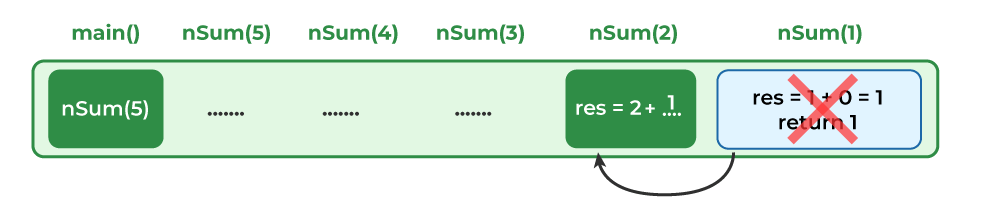

步骤8： 在nSum(2)中，nSum(1)调用将被其返回的值替换，即1。因此，在评估int res = 2 + 1, 3之后，将返回3给nSum(3)。同样的事情将继续发生，直到控制权再次回到nSum(5)。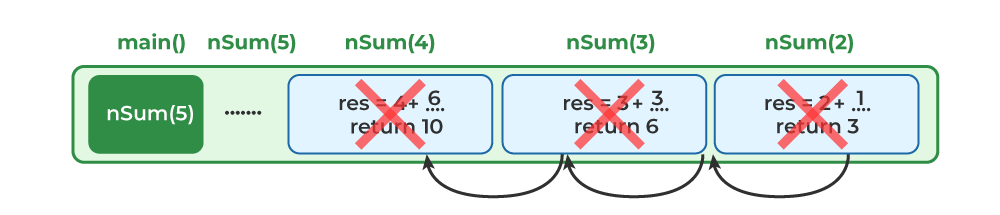

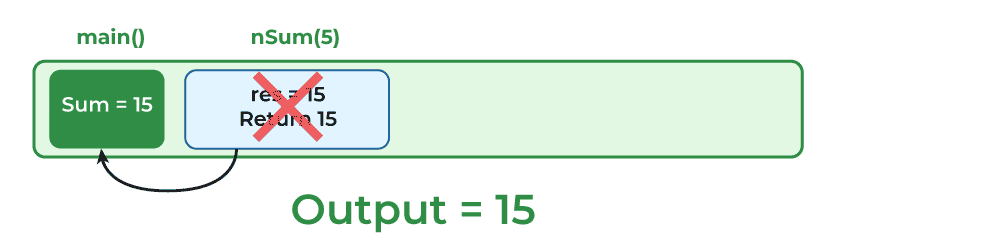
步骤9：当控制权到达nSum(5)时，表达式int res = 5 + nSum(4)将看起来像int res = 5 + 10。最后，这个值将被返回给main()函数，nSum()函数的执行将停止。

什么是堆栈溢出？¶

堆栈溢出是与递归相关的最常见错误之一，当函数调用自身太多次时会发生。正如我们所知，每个递归调用都需要在有限的堆栈内存中分配单独的空间。当有大量的递归调用或递归无限次进行时，堆栈内存可能会耗尽，无法存储更多数据，从而导致程序终止。

C++中的递归类型¶

有两种不同类型的递归，如下所示：

1. 直接递归
2. 间接递归

1. 直接递归¶

在直接递归中，函数包含一个或多个对自身的递归调用。函数在直接递归中直接调用自身，没有中间函数。直接递归也可以根据函数体中递归调用的方式和数量分为三种类型。

a) 头递归： 在头递归中，递归调用位于函数开头。它是一种线性递归，只使用一个递归调用。

b) 尾递归： 尾递归是一种线性递归，其中唯一的递归调用位于函数的末尾。递归调用通常是函数中的最后一个语句。尾递归的意义在于我们可以通过使用尾调用优化来减少其内存消耗。

c) 树递归： 在树递归中，函数体中存在多个递归调用。在跟踪树递归时，我们得到一个树状结构，其中多个递归调用从一个函数分支出来。

2. 间接递归¶

在间接递归中，函数不直接调用自身，而是调用另一个函数，然后该函数最终调用第一个函数，形成一个函数调用的循环。

C++递归示例¶

以下示例将提高对C++递归的理解：

示例1：使用递归的斐波那契数列¶

// C++ Program to find fibonacci series using recursion
#include <iostream>
using namespace std;

// Function for fibonacci
int fib(int n)
{
    // Stop condition
    if (n == 0)
        return 0;
    // Stop condition
    if (n == 1 || n == 2)
        return 1;
    // Recursion function
    else
        return (fib(n - 1) + fib(n - 2));
}

// Driver Code
int main()
{
    // Initialize variable n.
    int n = 5;
    cout << "Fibonacci series of 5 numbers is: ";
    // for loop to print the fibonacci series.
    for (int i = 0; i < n; i++) {
        cout << fib(i) << " ";
    }
    return 0;
}

输出

Fibonacci series of 5 numbers is: 0 1 1 2 3 

在这个示例中，Fibonacci函数使用较小的输入（n – 1和n – 2）调用自身，直到达到基本情况（n <= 1）并返回一个值。

示例2：使用递归逆序打印数组。¶

// C++ Program to print array using
// recursion
#include <iostream>
using namespace std;

// recursive function to print array
void pArray(int* arr, int n)
{
    // base condition
    if (n == 0) {
        return;
    }
    // recursive call
    cout << arr[n - 1] << ' ';
    pArray(arr, n - 1);  
}

int main()
{
    // declaring array
    int arr[5] = { 1, 2, 3, 4, 5 };
    // calling function
    pArray(arr, 5);
    return 0;
}

Output

5 4 3 2 1 

Applications of Recursion¶

递归在计算机科学和编程中有许多应用。以下是递归的一些最常见应用：

• 解决问题：斐波那契数列、阶乘函数、逆序数组、汉诺塔。
• 回溯：它是一种通过尝试不同的解决方案并在它们不起作用时撤销它们来解决问题的方法。递归算法通常用于回溯。
• 搜索和排序算法：许多搜索和排序算法，如二分搜索和快速排序，使用递归来将问题分解为更小的子问题。
• 树和图遍历：递归算法通常用于遍历树和图，如深度优先搜索和广度优先搜索。
• 数学计算：递归也用于许多数学计算，如阶乘函数和斐波那契数列。
• 动态规划：它是一种通过将问题分解为更小的子问题来解决优化问题的方法。递归算法通常用于动态规划。

总的来说，递归是一种强大且多功能的技巧，可用于解决编程和计算机科学中的广泛问题。

递归的缺点¶

• 性能：在某些情况下，递归算法可能不如迭代算法高效，特别是当数据结构很大或递归太深时。
• 内存使用：递归算法可能会使用大量内存，特别是当递归太深或数据结构很大时。每个递归调用在调用堆栈上创建一个新的堆栈帧，这可能会迅速增加到大量内存使用。
• 代码复杂性：递归算法可能比迭代算法更复杂。
• 调试：递归算法可能比迭代算法更难调试，特别是当递归太深或程序使用多个递归调用时。
• 堆栈溢出：如果递归太深，可能会导致堆栈溢出错误，从而导致程序崩溃。

总结¶

• 递归中有两种类型的案例，即递归案例和基本案例。
• 无限递归可能会导致堆栈内存耗尽。
• 每个递归调用都会在堆栈内存中创建该方法的新副本。
• 基本案例用于在案例为真时终止递归函数。
• 递归算法的示例：归并排序、快速排序、汉诺塔、斐波那契数列、阶乘问题等。

递归可以成为解决复杂问题的强大工具，但如果使用不当，它也可能效率低下并导致堆栈溢出错误。重要的是要谨慎使用递归，并确保在合理的时间内达到基本情况。

C++递归常见问题解答¶

Q1. 迭代和递归有什么区别？¶

答案：

递归和迭代都重复执行一组指令。它们之间的主要区别如下：

• 递归发生在函数中的语句反复调用自身时，而迭代发生在循环反复执行直到控制条件变为假时。
• 递归是始终应用于函数的过程，而迭代是应用于我们希望重复执行的一组指令的过程。

要了解更多区别，请参阅这篇文章 – 递归和迭代的区别

评论